Pseudocritics, and how not to be one

People on Twitter love to ridicule noisy-looking graphs. But very often, they're just misunderstanding the statistics

Here’s something I see happening on Twitter quite often:

• A researcher posts a scatterplot. Maybe it’s from their latest research project, or an interesting study they found.

• The scatterplot has a lot of dots in a big cloud, with no easily-discernible shape.

• There’s a line-of-best-fit through the points. Many of the dots are nowhere near the line - if you just looked at the dots alone you wouldn’t know if the line should be sloped upwards, downwards, or not sloped at all.

• The researcher claims a correlation between the two variables that are shown on the graph.

• Twitter users descend, saying things like: “lol, lmao”. They rarely state it explicitly, but what they mean is: “look at how random the points on this graph are! How can there possibly be any relation between these variables? Anyone claiming that there’s anything going on here must be truly idiotic! lol, lmao”.

This is the most recent instance I’ve seen:

John Protzko @JProtzko

About 3 weeks ago I thought: "I wonder if behavior on economic games has been getting more selfish over time. But doing that study would be A LOT of work." Thankfully, someone went through and found out 1956-2017, people have been getting less selfish apa.org/pubs/journals/…

Just take a look at some of the replies and quote-tweets. These people are laughing themselves silly at the (usually unstated) premise that a dataset like that simply couldn’t show a relation between the two variables (in this case, the variables are “co-operation rate” and “year”, and the claimed correlation is that cooperation increases over the years).

But this is a really basic misunderstanding of statistics - on the part of the critics. Let’s try and be charitable, and go through each of the arguments people might implicitly be making when they make fun of a graph like this.

Argument 1: The points are completely random and there’s no relationship between the variables. lol, lmao.

If you think this, you’re just flat-out wrong. Sorry about that. The reason we do statistics in the first place—actually calculating numbers, rather than just looking at graphs and trusting our intuition—is that it’s hard to tell signal from random noise. Maybe your undergrad statistics textbook made you think that graphs showing a relationship between variables always looked like this, where it’s very clear that the datapoints have a “shape”, which the best-fit line follows:

But in real life, datasets often look like the first graph above. That’s because in the real world there’s often a lot of statistical noise, and a lot of variation. That makes it harder to just “eyeball” a graph that pops up on Twitter and decide you know what the correlation is - but again, that’s why we have statistics. It’s simply the case that if you run a regression or correlation analysis on the “co-operation” and “year” variables from the study above, the statistics will tell you that there’s a correlation, and in this case that correlation is statistically significant.

On that basis, it’s absolutely fine to draw the interpretation “there is a correlation between co-operation and year”, as long as you also note that the correlation is weak: the reason it looks so messy and noisy, and the reason the correlation is hard to discern with the naked eye, is that it’s a really small correlation. Which leads us to…

Argument 2: There’s only a very weak correlation between the variables. lol, lmao.

It’s true that the correlation in the co-operation graph is weak. If you look at the paper, you find that it’s a correlation of r = .13; to use the standard phrasing, the year “explains 1.69% of the variance” in co-operation (that would be the R-squared). That’s not very much at all: more than 98% of the reasons co-operation varies in the dataset are nothing to do with what year it is! But it’s still completely fine to say that there’s a correlation, because correlations can be any size, and not every effect that’s of interest is a strong effect.

Now, you would be completely justified in slagging the paper off if the authors misrepresented the correlation - if they claimed or implied that it was a really strong effect when it so obviously isn’t. What do they actually say?

…we found a slight increase in cooperation over time.

Ah. From my reading, they’re mainly testing the idea that there’s been a decrease in co-operation over time; since in fact there’s if anything a (“slight”) increase, their data speak against this idea. They do go on to try and explain the increase, and you might argue some of the explanations are a bit of a stretch given how small the effect is. But there really doesn’t seem to be too much overhyping or misrepresentation going on here.

You could also be justified in your criticism if there were contextual reasons to believe this was a super-tiny effect, smaller than the normal effects found in this field. But it’s not clear that’s true here, either: in complex things like human psychology, small effects are the rule. If there were loads of large effects lying around, we’d be much better at doing things like solving people’s mental health problems and (perhaps scarily, at least sometimes) influencing their behaviour. We’re not very good at those things, because—among other reasons—the effects we discover tend to be small. If you discover a massive effect in a psychology study, the first thing to do is to check if you’ve made a mistake.

Depending on the context, small effects can be worthwhile. Think back to our recent discussion of nudges: if some hypothetical nudge that was very cheap to perform—sending a text message, say—had a small but reliable effect on people’s health behaviour—getting a vaccine, say—that would still be of interest, because it wouldn’t cost much to implement and would still have beneficial effects. Unless you know the context, criticising an effect for being small doesn’t make sense - it’s an over-application of a half-learned lesson from statistics that “effect size is important” (and it is: but what’s important is considering the effect size, because large and small effects can both matter).

There’s a final reason that it’s deeply misguided to attack the reporting of small effects just because they’re small effects. If a result is real, then you should publish it, regardless of whether it’s big or small, strong or weak. The idea that all results should be large ones is one of the main contributors to the replication crisis, where scientists (and scientific journals) developed an aversion to publishing weak effects, and an addiction to publishing effects that were super-strong - in many cases, too strong to be realistic. By ridiculing weak effects in this macho way—“haha, look at your puny little correlation!”—the critics are contributing to this totally toxic attitude.

Argument 3: There’s something about the way the points are distributed that makes the correlation spurious. lol, lmao.

This argument is more subtle, and I really am being charitable to imagine that it’s what the critical tweeters are saying. But let’s mention it anyway.

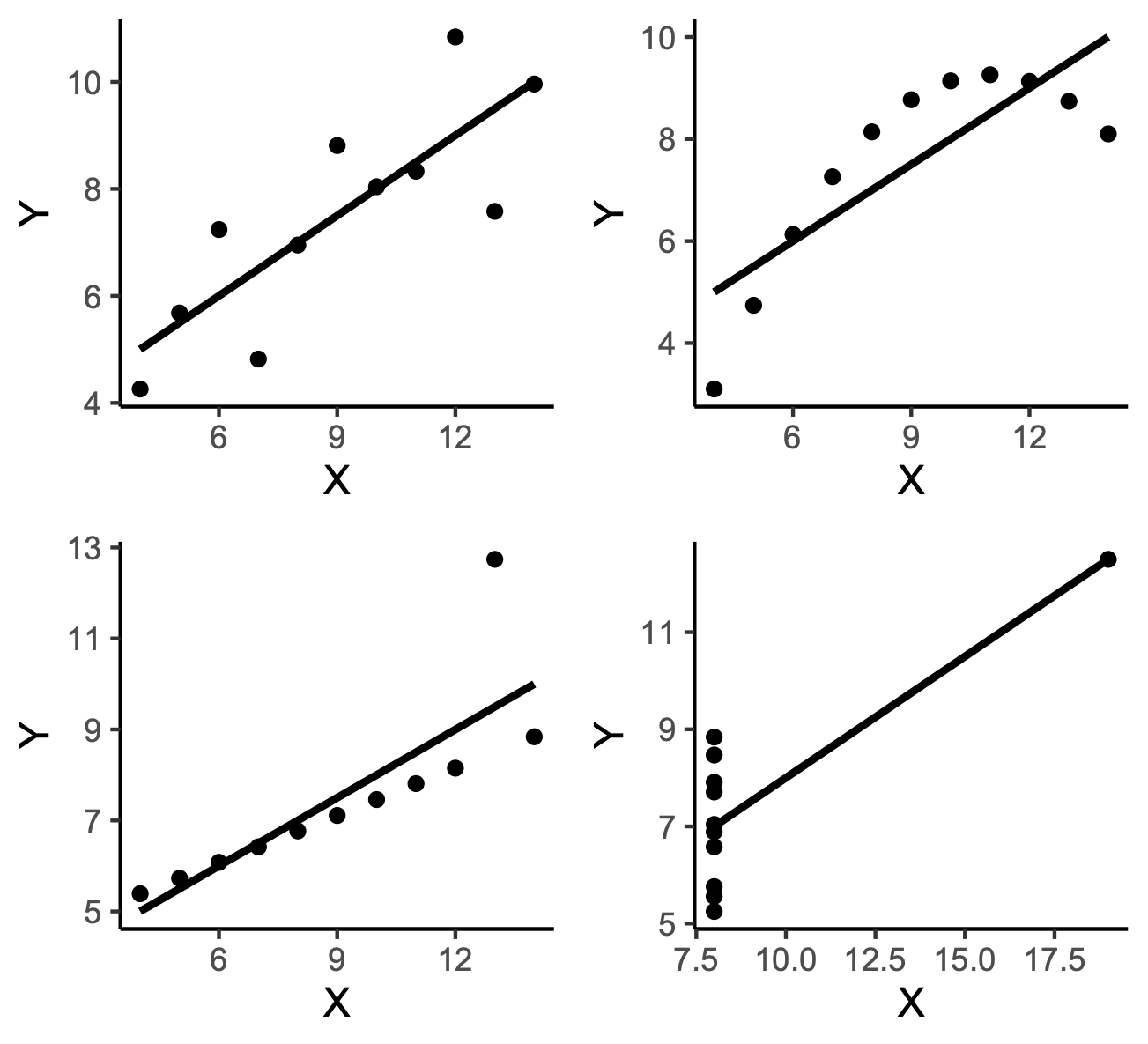
You might have seen the classic “Anscombe’s Quartet”. All four of the following graphs have the exact same correlation (and the equivalent variables have the exact same means and standard deviations), even though the distribution of the points—and the resulting interpretation of the data—is radically different in each one:

It would indeed be silly to say “there is a relationship between the variables” in some of these cases - for example in the bottom-right one, where the slope of the best-fit line is clearly entirely dependent on that single point in the top corner. Yes, statistically there’s a correlation, but it’s likely to be spurious and wouldn’t happen again if you replicated the study in a dataset that didn’t have that one weird single point.

Even if not as extreme as the examples in Anscombe’s Quartet, weird distributions can often undermine correlations and regressions. And it might well be the case that, were a few points to be different in the co-operation/year graph, the line would be different and the correlation would disappear. Weak correlations are, by their very nature, much more fragile, and more vulnerable to being wiped out by a few outlying datapoints. Or maybe there’s a non-linear relation between the variables, and a straight line does a bad job of representing how they’re linked.

It’s worth bearing in mind that some variables can look strange on a graph - for example, those that are ordinal (where there are a number of categories in order, like “no school qualifications” / “high school diploma” / “college degree” / “postgraduate qualification”). Yet it can still be completely fine to run a correlation on them, as long as you’re careful about exactly which stats you use (see, for example, the totally misplaced criticism of a graph about educational attainment in a genetic study earlier this year). Again, context is key.

In any case, first, I don’t see any particular reason to think that the co-operation graph is Anscombesque: the burden would be on the critic to show that the correlation doesn’t survive the removal of a few datapoints (the authors have put all their data online, so you can, as they say, go nuts), or that there’s something odd about the variables that changes the intepretation. And second, I’ve seen the “lol, lmao”-ers come for many different graphs that have no prominent outliers, and nothing obviously weird about the way the data are distributed. They really do seem to be exercised by the fact that the graph is noisy per se.

Just to be 100% clear: plotting the data before calculating a correlation is super-important, to avoid being fooled by the sorts of problems illustrated by Anscombe’s Quartet. This isn’t an argument that graphs don’t matter and you should only look at the statistics! It’s an argument to really think through your criticism - and to do that, you have to take into account the statistics, the graph, the claims made by the authors, and the overall context. One little tweet probably isn’t enough; “the graph looks noisy” is a heuristic that fails an awful lot of the time.

All these arguments look like scientific criticism of a study. The flurry of tweets looks like what happens when critics who know stats apply their knowledge to rightfully trash a piece of bad science. But in this and so many cases, it’s not real criticism: it’s pseudocriticism. It’s started by the misunderstanding of one or two people (the reason there were so many replies to the tweet above is because it was quote-tweeted by one of the biggest pseudocritics of them all, N.N. Taleb). Then, the majority of people afterwards simply take the initial critic’s word for it, joining in the “criticism” by just repeating what they said.

I’m sure it feels fun to do this - lord knows I enjoy pointing out low-quality research, and I’m sure I’ve provided some criticisms that were shallower than they should’ve been in the past. But pseudocriticism is empty calories - if we want our criticism to jibe with reality—and not just get clicks on Twitter—we need to put in at least a tiny bit more effort.

By the way, I don’t hold any particular brief for that study on co-operation. Maybe it’s really bad for some other reason: maybe the data included are low-quality, or there’s publication bias (it is a meta-analysis after all), or something else - I haven’t looked in detail. But as far as I could see they found a small—“slight”—correlation and discussed it as such, which really doesn’t set my alarm bells ringing.

So, the next time you feel like trashing a noisy-looking scatterplot, ask yourself what specifically is your problem with the graph, or with the way it’s been interpreted. If you can’t actually explain why you think it’s bad, if your explanation is unfair and unreasonable like Arguments 1 & 2 above, or if you’re just repeating what some other snarky tweeter has said without really understanding it, then maybe—just maybe—you’re a pseudocritic.

lol, lmao.

Image credits: Graphs (except the one in the tweet): the author.

Acknowledgements: I used the faux package for R to make the correlation in the X/Y graph above. The data for Anscombe’s Quartet are in the datasets package for R (original paper here). All graphs were made in ggplot.